| Physical cosmology | ||||||||
 | ||||||||
| Universe · Big Bang Age of the universe Timeline of the Big Bang Ultimate fate of the universe
| ||||||||
Two proposed forms for dark energy are the cosmological constant, a constant energy density filling space homogeneously,[3] and scalar fields such as quintessence or moduli, dynamic quantities whose energy density can vary in time and space. Contributions from scalar fields that are constant in space are usually also included in the cosmological constant. The cosmological constant is physically equivalent to vacuum energy. Scalar fields which do change in space can be difficult to distinguish from a cosmological constant because the change may be extremely slow.
High-precision measurements of the expansion of the universe are required to understand how the expansion rate changes over time. In general relativity, the evolution of the expansion rate is parameterized by the cosmological equation of state (the relationship between temperature, pressure, and combined matter, energy, and vacuum energy density for any region of space). Measuring the equation of state of dark energy is one of the biggest efforts in observational cosmology today.
Adding the cosmological constant to cosmology's standard FLRW metric leads to the Lambda-CDM model, which has been referred to as the "standard model" of cosmology because of its precise agreement with observations. Dark energy has been used as a crucial ingredient in a recent attempt to formulate a cyclic model for the universe.[4]
Contents
|
Evidence for dark energy
Supernovae
In 1998, published observations of Type Ia supernovae ("one-A") by the High-z Supernova Search Team [5] followed in 1999 by the Supernova Cosmology Project [6] suggested that the expansion of the universe is accelerating.[7] Since then, these observations have been corroborated by several independent sources. Measurements of the cosmic microwave background, gravitational lensing, and the large scale structure of the cosmos as well as improved measurements of supernovae have been consistent with the Lambda-CDM model.[8]Supernovae are useful for cosmology because they are excellent standard candles across cosmological distances. They allow the expansion history of the Universe to be measured by looking at the relationship between the distance to an object and its redshift, which gives how fast it is receding from us. The relationship is roughly linear, according to Hubble's law. It is relatively easy to measure redshift, but finding the distance to an object is more difficult. Usually, astronomers use standard candles: objects for which the intrinsic brightness, the absolute magnitude, is known. This allows the object's distance to be measured from its actual observed brightness, or apparent magnitude. Type Ia supernovae are the best-known standard candles across cosmological distances because of their extreme, and extremely consistent, brightness.
Recent observations of supernovae are consistent with a universe made up 71.3% of dark energy and 27.4% of a combination of dark matter and baryonic matter.[9]
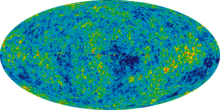
Cosmic Microwave Background
The existence of dark energy, in whatever form, is needed to reconcile the measured geometry of space with the total amount of matter in the universe. Measurements of cosmic microwave background (CMB) anisotropies, most recently by the WMAP spacecraft, indicate that the universe is close to flat. For the shape of the universe to be flat, the mass/energy density of the universe must be equal to a certain critical density. The total amount of matter in the universe (including baryons and dark matter), as measured by the CMB, accounts for only about 30% of the critical density. This implies the existence of an additional form of energy to account for the remaining 70%.[8] The WMAP five-year analysis estimate a universe made up of 74% dark energy, 22% dark matter, and 4% ordinary matter.[10] More recently, the WMAP seven-year analysis gave an estimate of 72.8% dark energy, 22.7% dark matter and 4.6% ordinary matter.[2]Large-Scale Structure
The theory of large scale structure, which governs the formation of structures in the universe (stars, quasars, galaxies and galaxy clusters), also suggests that the density of matter in the universe is only 30% of the critical density.Late-time Integrated Sachs-Wolfe Effect
Accelerated cosmic expansion causes gravitational potential wells and hills to flatten as photons pass through them, producing cold spots and hot spots on the CMB aligned with vast supervoids and superclusters. This so-called late-time Integrated Sachs-Wolfe effect (ISW) is a direct signal of dark energy in a flat universe,[11] and has recently been detected at high significance by Ho et al.[12] and Giannantonio et al.[13]Nature of dark energy
The nature of this dark energy is a matter of speculation. It is known to be very homogeneous, not very dense and is not known to interact through any of the fundamental forces other than gravity. Since it is not very dense—roughly 10−29 grams per cubic centimeter—it is hard to imagine experiments to detect it in the laboratory. Dark energy can only have such a profound impact on the universe, making up 74% of universal density, because it uniformly fills otherwise empty space. The two leading models are quintessence and the cosmological constant. Both models include the common characteristic that dark energy must have negative pressure.Negative pressure
Independently from its actual nature, dark energy would need to have a strong negative pressure (i.e. effects, acting repulsively) in order to explain the observed acceleration in the expansion rate of the universe.According to General Relativity, the pressure within a substance contributes to its gravitational attraction for other things just as its mass density does. This happens because the physical quantity that causes matter to generate gravitational effects is the Stress-energy tensor, which contains both the energy (or matter) density of a substance and its pressure and viscosity.
In the Friedmann-Lemaître-Robertson-Walker metric, it can be shown that a strong constant negative pressure in all the universe causes an acceleration in universe expansion if the universe is already expanding, or a deceleration in universe contraction if the universe is already contracting. More exactly, the second derivative of the universe scale factor,
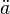 , is positive if the equation of state of the universe is such that
, is positive if the equation of state of the universe is such that  .
.This accelerating expansion effect is sometimes labeled "gravitational repulsion", which is a colorful but possibly confusing expression. In fact a negative pressure does not influence the gravitational interaction between masses—which remains attractive—but rather alters the overall evolution of the universe at the cosmological scale, typically resulting in the accelerating expansion of the universe despite the attraction among the masses present in the universe.
Cosmological constant
Main article: Cosmological constant
For more details on this topic, see Equation of state (cosmology).
The simplest explanation for dark energy is that it is simply the "cost of having space": that is, a volume of space has some intrinsic, fundamental energy. This is the cosmological constant, sometimes called Lambda (hence Lambda-CDM model) after the Greek letter Λ, the symbol used to mathematically represent this quantity. Since energy and mass are related by E = mc2, Einstein's theory of general relativity predicts that it will have a gravitational effect. It is sometimes called a vacuum energy because it is the energy density of empty vacuum. In fact, most theories of particle physics predict vacuum fluctuations that would give the vacuum this sort of energy. This is related to the Casimir Effect, in which there is a small suction into regions where virtual particles are geometrically inhibited from forming (e.g. between plates with tiny separation). The cosmological constant is estimated by cosmologists to be on the order of 10−29g/cm³, or about 10−120 in reduced Planck units. However, particle physics predicts a natural value of 1 in reduced Planck units, a large discrepancy which is still not explained.The cosmological constant has negative pressure equal to its energy density and so causes the expansion of the universe to accelerate. The reason why a cosmological constant has negative pressure can be seen from classical thermodynamics; Energy must be lost from inside a container to do work on the container. A change in volume dV requires work done equal to a change of energy −p dV, where p is the pressure. But the amount of energy in a box of vacuum energy actually increases when the volume increases (dV is positive), because the energy is equal to ρV, where ρ (rho) is the energy density of the cosmological constant. Therefore, p is negative and, in fact, p = −ρ.
A major outstanding problem is that most quantum field theories predict a huge cosmological constant from the energy of the quantum vacuum, more than 100 orders of magnitude too large.[14][verification needed] This would need to be cancelled almost, but not exactly, by an equally large term of the opposite sign. Some supersymmetric theories require a cosmological constant that is exactly zero, which does not help. The present scientific consensus amounts to extrapolating the empirical evidence where it is relevant to predictions, and fine-tuning theories until a more elegant solution is found. Technically, this amounts to checking theories against macroscopic observations. Unfortunately, as the known error-margin in the constant predicts the fate of the universe more than its present state, many such "deeper" questions remain unknown.
Another problem arises with inclusion of the cosmological constant in the standard model: i.e., the appearance of solutions with regions of discontinuities (see classification of discontinuities for three examples) at low matter density.[15] Discontinuity also affects the past sign of the pressure assigned to the cosmological constant, changing from the current negative pressure to attractive, as one looks back towards the early Universe. A systematic, model-independent evaluation of the supernovae data supporting inclusion of the cosmological constant in the standard model indicates these data suffer systematic error. The supernovae data are not overwhelming evidence for an accelerating Universe expansion which may be simply gliding.[16] A numerical evaluation of WMAP and supernovae data for evidence that our local group exists in a local void with poor matter density compared to other locations, uncovered possible conflict in the analysis used to support the cosmological constant.[17] A recent theoretical investigation found the cosmological time, dt, diverges for any finite interval, ds, associated with an observer approaching the cosmological horizon, representing a physical limit to observation. This is a key component required for a complete interpretation of astronomical observations, particularly pertaining to the nature of dark energy.[18] The identification of dark energy as a cosmological constant does not appear to be consistent with the data. These findings should be considered shortcomings of the standard model, but only when a term for vacuum energy is included.
In spite of its problems, the cosmological constant is in many respects the most economical solution to the problem of cosmic acceleration. One number successfully explains a multitude of observations. Thus, the current standard model of cosmology, the Lambda-CDM model, includes the cosmological constant as an essential feature.
Quintessence
Main article: Quintessence (physics)
In quintessence models of dark energy, the observed acceleration of the scale factor is caused by the potential energy of a dynamical field, referred to as quintessence field. Quintessence differs from the cosmological constant in that it can vary in space and time. In order for it not to clump and form structure like matter, the field must be very light so that it has a large Compton wavelength.No evidence of quintessence is yet available, but it has not been ruled out either. It generally predicts a slightly slower acceleration of the expansion of the universe than the cosmological constant. Some scientists think that the best evidence for quintessence would come from violations of Einstein's equivalence principle and variation of the fundamental constants in space or time. Scalar fields are predicted by the standard model and string theory, but an analogous problem to the cosmological constant problem (or the problem of constructing models of cosmic inflation) occurs: renormalization theory predicts that scalar fields should acquire large masses.
The cosmic coincidence problem asks why the cosmic acceleration began when it did. If cosmic acceleration began earlier in the universe, structures such as galaxies would never have had time to form and life, at least as we know it, would never have had a chance to exist. Proponents of the anthropic principle view this as support for their arguments. However, many models of quintessence have a so-called tracker behavior, which solves this problem. In these models, the quintessence field has a density which closely tracks (but is less than) the radiation density until matter-radiation equality, which triggers quintessence to start behaving as dark energy, eventually dominating the universe. This naturally sets the low energy scale of the dark energy.
In 2004, when scientists fit the evolution of dark energy with the cosmological data, they found that the equation of state had possibly crossed the cosmological constant boundary (w=-1) from above to below. A No-Go theorem has been proved that to give this scenario at least two degrees of freedom are required for dark energy models. This scenario is so-called Quintom scenario.
Some special cases of quintessence are phantom energy, in which the energy density of quintessence actually increases with time, and k-essence (short for kinetic quintessence) which has a non-standard form of kinetic energy. They can have unusual properties: phantom energy, for example, can cause a Big Rip.
Alternative ideas
Some theorists think that dark energy and cosmic acceleration are a failure of general relativity on very large scales, larger than superclusters.[citation needed] However most attempts at modifying general relativity have turned out to be either equivalent to theories of quintessence, or inconsistent with observations.[citation needed]Alternative ideas for dark energy have come from string theory, brane cosmology and the holographic principle, but have not yet proved[citation needed] as compelling as quintessence and the cosmological constant.
On string theory, an article in the journal Nature described:
String theories, popular with many particle physicists, make it possible, even desirable, to think that the observable universe is just one of 10500 universes in a grander multiverse, says [Leonard Susskind, a cosmologist at Stanford University in California]. The vacuum energy will have different values in different universes, and in many or most it might indeed be vast. But it must be small in ours because it is only in such a universe that observers such as ourselves can evolve.[14]Paul Steinhardt in the same article criticizes string theory's explanation of dark energy stating "...Anthropics and randomness don't explain anything... I am disappointed with what most theorists are willing to accept".[14]
Yet another, "radically conservative" class of proposals aims to explain the observational data by a more refined use of established theories rather than through the introduction of dark energy, focusing, for example, on the gravitational effects of density inhomogeneities, or on consequences of electroweak symmetry breaking in the early universe. If we are located in an emptier-than-average region of space, the observed cosmic expansion rate could be mistaken for a variation in time, or acceleration.[19][20][21]
Another class of theories attempts to come up with an all-encompassing theory of both Dark Matter and Dark Energy as a single phenomenon that modifies the laws of gravity at various scales. An example of this type of theory is the theory of Dark Fluid. Another class of theories that unifies Dark Matter and Dark Energy are suggested to be covariant theories of modified gravities. These theories alter the dynamics of the space-time such that the modified dynamic stems what have been assigned to the presence of Dark Energy and Dark matter.[22]
Another set of proposals is based on the possibility of a double metric tensor for space-time.[23][24] It has been argued that time reversed solutions in general relativity require such double metric for consistency, and that both Dark Matter and Dark Energy can be understood in terms of time reversed solutions of general relativity.[25]
Implications for the fate of the universe
Cosmologists estimate that the acceleration began roughly 5 billion years ago. Before that, it is thought that the expansion was decelerating, due to the attractive influence of dark matter and baryons. The density of dark matter in an expanding universe decreases more quickly than dark energy, and eventually the dark energy dominates. Specifically, when the volume of the universe doubles, the density of dark matter is halved but the density of dark energy is nearly unchanged (it is exactly constant in the case of a cosmological constant).If the acceleration continues indefinitely, the ultimate result will be that galaxies outside the local supercluster will have a line-of-sight velocity that continually increases with time, eventually far exceeding the speed of light.[26] This is not a violation of special relativity, because the notion of "velocity" used here is different from that of velocity in a local inertial frame of reference, which is still constrained to be less than the speed of light for any massive object (see Comoving distance#Uses of the proper distance for a discussion of the subtleties of defining any notion of relative velocity in cosmology). Because the Hubble parameter is decreasing with time, there can actually be cases where a galaxy that is receding from us faster than light does manage to emit a signal which reaches us eventually.[27][28] However, because of the accelerating expansion, it is projected that most galaxies will eventually cross a type of cosmological event horizon where any light they emit past that point will never be able to reach us at any time in the infinite future,[29] because the light never reaches a point where its "peculiar velocity" towards us exceeds the expansion velocity away from us (these two notions of velocity are also discussed in Comoving distance#Uses of the proper distance). Assuming the dark energy is constant (a cosmological constant), the current distance to this cosmological event horizon is about 16 billion light years, meaning that a signal from an event happening at present would eventually be able to reach us in the future if the event was less than 16 billion light years away, but the signal would never reach us if the event was more than 16 billion light years away.[28]
As galaxies approach the point of crossing this cosmological event horizon, the light from them will become more and more redshifted, to the point where the wavelength becomes too large to detect in practice and the galaxies appear to disappear completely.[30][31] (see Future of an expanding universe#Galaxies outside the Local Supercluster are no longer detectable) The Earth, the Milky Way and the Virgo supercluster, however, would remain virtually undisturbed while the rest of the universe recedes and disappears from view. In this scenario, the local supercluster would ultimately suffer heat death, just as was thought for the flat, matter-dominated universe, before measurements of cosmic acceleration.
There are some very speculative ideas about the future of the universe. One suggests that phantom energy causes divergent expansion, which would imply that the effective force of dark energy continues growing until it dominates all other forces in the universe. Under this scenario, dark energy would ultimately tear apart all gravitationally bound structures, including galaxies and solar systems, and eventually overcome the electrical and nuclear forces to tear apart atoms themselves, ending the universe in a "Big Rip". On the other hand, dark energy might dissipate with time, or even become attractive. Such uncertainties leave open the possibility that gravity might yet rule the day and lead to a universe that contracts in on itself in a "Big Crunch". Some scenarios, such as the cyclic model suggest this could be the case. While these ideas are not supported by observations, they are not ruled out. Measurements of acceleration are crucial to determining the ultimate fate of the universe in big bang theory.
History
Alan Guth proposed in the 1970s that a negative pressure field, similar in concept to dark energy, could drive cosmic inflation in the very early universe. Inflation postulates that some repulsive force, qualitatively similar to dark energy, resulted in an enormous and exponential expansion of the universe slightly after the Big Bang. Such expansion is an essential feature of most current models of the Big Bang. However, inflation must have occurred at a much higher energy density than the dark energy we observe today and is thought to have completely ended when the universe was just a fraction of a second old. It is unclear what relation, if any, exists between dark energy and inflation. Even after inflationary models became accepted, the cosmological constant was thought to be irrelevant to the current universe.
The term "dark energy", echoing Fritz Zwicky's "dark matter" from the 1930s, was coined by Michael Turner in 1998.[32] By that time, the missing mass problem of big bang nucleosynthesis and large scale structure was established, and some cosmologists had started to theorize that there was an additional component to our universe. The first direct evidence for dark energy came from supernova observations of accelerated expansion, in Riess et al.[5] and later confirmed in Perlmutter et al.[6] This resulted in the Lambda-CDM model, which as of 2006 is consistent with a series of increasingly rigorous cosmological observations, the latest being the 2005 Supernova Legacy Survey. First results from the SNLS reveal that the average behavior (i.e., equation of state) of dark energy behaves like Einstein's cosmological constant to a precision of 10%.[33] Recent results from the Hubble Space Telescope Higher-Z Team indicate that dark energy has been present for at least 9 billion years and during the period preceding cosmic acceleration.


No comments:
Post a Comment