Avogadro's law (sometimes referred to as Avogadro's hypothesis or Avogadro's principle) is a gas law named after Amedeo Avogadro who, in 1811,[1] hypothesized that two given samples of an ideal gas, at the same temperature, pressure and volume, contain the same number of molecules. Thus, the number of molecules or atoms in a specific volume of gas is independent of their size or the molar mass of the gas.
As an example, equal volumes of molecular hydrogen and nitrogen contain the same number of molecules when they are at the same temperature and pressure, and observe ideal gas behavior. In practice, real gases show small deviations from the ideal behavior and the law holds only approximately, but is still a useful approximation for scientists.
As an example, equal volumes of molecular hydrogen and nitrogen contain the same number of molecules when they are at the same temperature and pressure, and observe ideal gas behavior. In practice, real gases show small deviations from the ideal behavior and the law holds only approximately, but is still a useful approximation for scientists.
Contents |
Mathematical definition
Avogadro's law is stated mathematically as:- V is the volume of the gas.
- n is the amount of substance of the gas.
- k is a proportionality constant.
- p is the pressure of the gas
- T is the temperature in kelvin of the gas
Ideal gas law
A common rearrangement of this equation is by letting R be the proportionality constant, and rearranging as follows:- pV = nRT

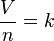


No comments:
Post a Comment