Charles's law (also known as the law of volumes) is an experimental gas law which describes how gases tend to expand when heated. It was first published by French natural philosopher Joseph Louis Gay-Lussac in 1802,[1] although he credited the discovery to unpublished work from the 1780s by Jacques Charles. The law was independently discovered by British natural philosopher John Dalton by 1801, although Dalton's description was less thorough than Gay-Lussac's.[2] The basic principles had already been described a century earlier by Guillaume Amontons.
Gay-Lussac was the first to demonstrate that the law applied generally to all gases, and also to the vapours of volatile liquids if the temperature was more than a few degrees above the boiling point.[citation needed] His statement of the law can be expressed mathematically as:
A modern statement of Charles's law is:
This law of volumes implies theoretically that as a temperature reaches absolute zero the gas will shrink down to zero volume. This is not physically correct, since in fact all gases turn into liquids at a low enough temperature, and Charles' law is not applicable at low temperatures for this reason.
The fact that the gas will occupy a non-zero volume - even as the temperature approaches absolute zero - arises fundamentally from the uncertainty principle of quantum theory. However, as the temperature is reduced, gases turn into liquids long before the limits of the uncertainty principle come into play due to the attractive forces between molecules which are neglected by Charles's Law.
The modern statement of the ideal gas law is:
An ideal gas is defined as a gas which obeys the ideal gas law, so Charles's law is only expected to be followed exactly by ideal gases. Nevertheless, it is a good approximation to the behaviour of real gases at relatively high temperatures and relatively low pressures.
Gay-Lussac was the first to demonstrate that the law applied generally to all gases, and also to the vapours of volatile liquids if the temperature was more than a few degrees above the boiling point.[citation needed] His statement of the law can be expressed mathematically as:
A modern statement of Charles's law is:
At constant pressure, the volume of a given mass of an ideal gas increases or decreases by the same factor as its temperature on the absolute temperature scale (i.e. the gas expands as the temperature increases).[3]which can be written as:
Contents |
Limitations
In modern physics, Charles's Law is seen as a special case of the ideal gas equation, in which the pressure and number of molecules are held constant. The ideal gas equation is usually derived from the kinetic theory of gases, which presumes that molecules occupy negligible volume, do not attract each other and undergo elastic collisions (no loss of kinetic energy); an imaginary gas with exactly these properties is termed an ideal gas. The behavior of a real gas is close to that of an ideal gas under most circumstances, which makes the ideal gas law useful.This law of volumes implies theoretically that as a temperature reaches absolute zero the gas will shrink down to zero volume. This is not physically correct, since in fact all gases turn into liquids at a low enough temperature, and Charles' law is not applicable at low temperatures for this reason.
The fact that the gas will occupy a non-zero volume - even as the temperature approaches absolute zero - arises fundamentally from the uncertainty principle of quantum theory. However, as the temperature is reduced, gases turn into liquids long before the limits of the uncertainty principle come into play due to the attractive forces between molecules which are neglected by Charles's Law.
Relation to the ideal gas law
French physicist Émile Clapeyron combined Charles's law with Boyle's law in 1834 to produce a single statement which would become known as the ideal gas law.[4] Claypeyron's original statement was:The modern statement of the ideal gas law is:
An ideal gas is defined as a gas which obeys the ideal gas law, so Charles's law is only expected to be followed exactly by ideal gases. Nevertheless, it is a good approximation to the behaviour of real gases at relatively high temperatures and relatively low pressures.
Relation to absolute zero
Charles's law appears to imply that the volume of a gas will descend to zero at a certain temperature (−266.66 °C according to Gay-Lussac's figures)or -273°C. Gay-Lussac was clear in his description that the law was not applicable at low temperatures:but I may mention that this last conclusion cannot be true except so long as the compressed vapors remain entirely in the elastic state; and this requires that their temperature shall be sufficiently elevated to enable them to resist the pressure which tends to make them assume the liquid state.[1]Gay-Lussac had no experience of liquid air (first prepared in 1877), although he appears to believe (as did Dalton) that the "permanent gases" such as air and hydrogen could be liquified. Gay-Lussac had also worked with the vapours of volatile liquids in demonstrating Charles' law, and was aware that the law does not apply just above the boiling point of the liquid:
I may however remark that when the temperature of the ether is only a little above its boiling point, its condensation is a little more rapid than that of atmospheric air. This fact is related to a phenomenon which is exhibited by a great many bodies when passing from the liquid to the solid state, but which is no longer sensible at temperatures a few degrees above that at which the transition occurs.[1]The first mention of a temperature at which the volume of a gas might descend to zero was by William Thomson (later known as Lord Kelvin) in 1848:[5]
This is what we might anticipate, when we reflect that infinite cold must correspond to a finite number of degrees of the air-thermometer below zero; since if we push the strict principle of graduation, stated above, sufficiently far, we should arrive at a point corresponding to the volume of air being reduced to nothing, which would be marked as −273° of the scale (−100/.366, if .366 be the coefficient of expansion); and therefore −273° of the air-thermometer is a point which cannot be reached at any finite temperature, however low.However, the "absolute zero" on the Kelvin temperature scale was originally defined in terms of the second law of thermodynamics, which Thomson himself described in 1852.[6] Thomson did not assume that this was equal to the "zero-volume point" of Charles's law, merely that Charles's law provided the minimum temperature which could be attained. The two can be shown to be equivalent by Ludwig Boltzmann's statistical view of entropy (1870).


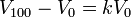



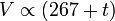
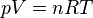
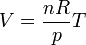

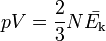
No comments:
Post a Comment