| Classical mechanics | ||||||
History of classical mechanics · Timeline of classical mechanics
| ||||||
| | |
| SI symbol: | p |
| SI unit: | kg · m/s |
| Conserved: | yes |
| Derivations from other quantities: | p = mv p = γm0v |
Although originally expressed in Newton's Second Law, the conservation of momentum also holds in special relativity, and with appropriate definitions a (generalized) momentum conservation law holds in electrodynamics, quantum mechanics, quantum field theory, and general relativity. In relativistic mechanics, momentum is further multiplied by the Lorentz factor.
Contents |
History of the concept
Mōmentum was not merely the motion, which was mōtus, but was the power residing in a moving object, captured by today's mathematical definitions. A mōtus, "movement", was a stage in any sort of change,[1] while velocitas, "swiftness", captured only speed. The concept of momentum in classical mechanics was originated by a number of great thinkers and experimentalists. The first of these was Byzantine philosopher John Philoponus, in his commentary to Aristotle´s Physics. As regards the natural motion of bodies falling through a medium, Aristotle's verdict that the speed is proportional to the weight of the moving bodies and indirectly proportional to the density of the medium is disproved by Philoponus through appeal to the same kind of experiment that Galileo was to carry out centuries later.[2] This idea was refined by the European philosophers Peter Olivi and Jean Buridan. Buridan referred to impetus being proportional to the weight times the speed.[3][4] Moreover, Buridan´s theory was different to his predecessor´s in that he did not consider impetus to be self dissipating, asserting that a body would be arrested by the forces of air resistance and gravity which might be opposing its impetus.[5]René Descartes believed that the total "quantity of motion" in the universe is conserved, where the quantity of motion is understood as the product of size and speed. This should not be read as a statement of the modern law of momentum, since he had no concept of mass as distinct from weight and size, and more importantly he believed that it is speed rather than velocity that is conserved. So for Descartes if a moving object were to bounce off a surface, changing its direction but not its speed, there would be no change in its quantity of motion.[6] Galileo, later, in his Two New Sciences, used the Italian word "impeto".
The extent to which Isaac Newton contributed to the concept has been much debated. The answer is apparently nothing, except to state more fully and with better mathematics what was already known. Yet for scientists, this was the death knell for Aristotelian physics and supported other progressive scientific theories (i.e., Kepler's laws of planetary motion). Conceptually, the first and second of Newton's Laws of Motion had already been stated by John Wallis in his 1670 work, Mechanica sive De Motu, Tractatus Geometricus: "the initial state of the body, either of rest or of motion, will persist" and "If the force is greater than the resistance, motion will result".[7] Wallis uses momentum and vis for force. Newton's Philosophiæ Naturalis Principia Mathematica, when it was first published in 1687, showed a similar casting around for words to use for the mathematical momentum. His Definition II[8] defines quantitas motus, "quantity of motion", as "arising from the velocity and quantity of matter conjointly", which identifies it as momentum.[9] Thus when in Law II he refers to mutatio motus, "change of motion", being proportional to the force impressed, he is generally taken to mean momentum and not motion.[10] It remained only to assign a standard term to the quantity of motion. The first use of "momentum" in its proper mathematical sense is not clear but by the time of Jenning's Miscellanea in 1721, four years before the final edition of Newton's Principia Mathematica, momentum M or "quantity of motion" was being defined for students as "a rectangle", the product of Q and V, where Q is "quantity of material" and V is "velocity", s/t.[11]
Some languages, such as French still lack a single term for momentum, and use a phrase such as the literal translation of "quantity of motion". In Bulgarian and in Dutch the linear momentum is typically referred to as impulse, while the angular momentum is called momentum and the impulse has no distinct name.
Linear momentum of a particle
The amount of momentum that an object has depends on two physical quantities: the mass and the velocity of the moving object in the frame of reference. In physics, the usual symbol for momentum is a bold p (bold because it is a vector); so this can be written
Example: a model airplane of 1 kg traveling due north at 1 m/s in straight and level flight has a momentum of 1 kg·m/s due north measured from the ground. To the dummy pilot in the cockpit it has a velocity and momentum of zero.
According to Newton's second law, the rate of change of the momentum of a particle is proportional to the resultant force acting on the particle and is in the direction of that force. The derivation of force from momentum is given below.
 ). We can therefore write the following:
). We can therefore write the following:Example: a model airplane of 1 kg accelerates from rest to a velocity of 1 m/s due north in 1 s. The thrust required to produce this acceleration is 1 newton. The change in momentum is 1 kg·m/s. To the dummy pilot in the cockpit there is no change of momentum. Its pressing backward in the seat is a reaction to the unbalanced thrust, shortly to be balanced by the drag.
Linear momentum of a system of particles
Relating to mass and velocity
The linear momentum of a system of particles is the vector sum of the momenta of all the individual objects in the system:It can be shown that, in the center of mass frame the momentum of a system is zero. Additionally, the momentum in a frame of reference that is moving at a velocity vcm with respect to that frame is simply:
Relating to force - General equations of motion
The linear momentum of a system of particles can also be defined as the product of the total mass, m, of the system times the velocity, vcm, of the center of mass.For a more general derivation using tensors, we consider a moving body (see Figure), assumed as a continuum, occupying a volume V, at a time t, having a surface area S, with defined traction or surface forces per unit area represented by the stress vector
 acting on every point of every body surface (external and internal), body forces Fi per unit of volume on every point within the volume V, and a velocity field vi, prescribed throughout the body. Following the previous equation, the linear momentum of the system is:
acting on every point of every body surface (external and internal), body forces Fi per unit of volume on every point within the volume V, and a velocity field vi, prescribed throughout the body. Following the previous equation, the linear momentum of the system is: , then
, then as the differential operator):
as the differential operator): Plugging this into the previous equation, and rearranging the terms, we get:
Plugging this into the previous equation, and rearranging the terms, we get:If a system is in equilibrium, the change in momentum with respect to time is equal to 0, as there is no acceleration
Conservation of linear momentum
The law of conservation of linear momentum is a fundamental law of nature, and it states that if no external force acts on a closed system of objects the momentum of the closed system is constant. One of the consequences of this is that the center of mass of any system of objects will always continue with the same velocity unless acted on by a force from outside the system.Conservation of momentum is a mathematical consequence of the homogeneity (shift symmetry) of space (position in space is the canonical conjugate quantity to momentum). So, momentum conservation can be philosophically stated as "nothing depends on location per se".
In analytical mechanics the conservation of momentum is a consequence of translational invariance of Lagrangian in the absence of external forces. It can be proven that the total momentum is a constant of motion by making an infinitesimal translation of Lagrangian and then equating it with non translated Lagrangian. This is a special case of Noether's theorem .[14]
In an isolated system (one where external forces are absent) the total momentum will be constant: this is implied by Newton's first law of motion. Newton's third law of motion, the law of reciprocal actions, which dictates that the forces acting between systems are equal in magnitude, but opposite in sign, is due to the conservation of momentum.
Since position in space is a vector quantity, momentum (being the canonical conjugate of position) is a vector quantity as well—it has direction. Thus, when a gun is fired, the final total momentum of the system (the gun and the bullet) is the vector sum of the momenta of these two objects. Assuming that the gun and bullet were at rest prior to firing (meaning the initial momentum of the system was zero), the final total momentum must also equal 0.
In an isolated system with only two objects, the change in momentum of one object must be equal and opposite to the change in momentum of the other object. Mathematically,
A common problem in physics that requires the use of this fact is the collision of two particles. Since momentum is always conserved, the sum of the momenta before the collision must equal the sum of the momenta after the collision:
Determining the final velocities from the initial velocities (and vice versa) depend on the type of collision. There are two types of collisions that conserve momentum: elastic collisions, which also conserve kinetic energy, and inelastic collisions, which do not.
Elastic collisions
A collision between two pool balls is a good example of an almost totally elastic collision, due to their high rigidity; a totally elastic collision exists only in theory, occurring between bodies with mathematically infinite rigidity. In addition to momentum being conserved when the two balls collide, the sum of kinetic energy before a collision must equal the sum of kinetic energy after:In one dimension
When the initial velocities are known, the final velocities for a head-on collision are given by
A Newton's cradle demonstrates conservation of momentum.
In multiple dimensions
In the case of objects colliding in more than one dimension, as in oblique collisions, the velocity is resolved into orthogonal components with one component perpendicular to the plane of collision and the other component or components in the plane of collision. The velocity components in the plane of collision remain unchanged, while the velocity perpendicular to the plane of collision is calculated in the same way as the one-dimensional case.For example, in a two-dimensional collision, the momenta can be resolved into x and y components. We can then calculate each component separately, and combine them to produce a vector result. The magnitude of this vector is the final momentum of the isolated system.
Perfectly inelastic collisions
A common example of a perfectly inelastic collision is when two snowballs collide and then stick together afterwards. This equation describes the conservation of momentum:[edit] Coefficient of Restitution
Main article: Coefficient of Restitution
The coefficient of restitution is defined as the ratio of relative velocity of separation to relative velocity of approach. It is a ratio hence it is a dimensionless quantity. The coefficient of restitution is given by:- v1 is the scalar final velocity of the first object after impact
- v2 is the scalar final velocity of the second object after impact
- u1 is the scalar initial velocity of the first object before impact
- u2 is the scalar initial velocity of the second object before impact.
Inelastic collisions have (CR < 1). In case of a perfectly inelastic collision the relative velocity of separation of the centre of masses of the colliding bodies is 0. Hence the bodies stick together after collision.
Explosions
An explosion occurs as a result of a chain reaction that transforms potential energy into kinetic energy displacing the surrounding material. Explosions do not conserve potential energy. Instead, potential energy stored in chemical, mechanical, or nuclear form, is transformed into kinetic energy, acoustic energy, and electromagnetic radiation.See the inelastic collision page for more details.
Modern definitions of momentum
Momentum in relativistic mechanics
In relativistic mechanics, in order to be conserved, the momentum of an object must be defined as is the magnitude of the momentum.
is the magnitude of the momentum.Relativistic momentum can also be written as invariant mass times the object's proper velocity, defined as the rate of change of object position in the observer frame with respect to time elapsed on object clocks (i.e. object proper time). Within the domain of classical mechanics, relativistic momentum closely approximates Newtonian momentum: at low velocity, γm0v is approximately equal to m0v, the Newtonian expression for momentum.

A graphical representation of the interrelation of relativistic energy E, invariant mass m0, relativistic momentum p, and relativistic mass m = γm0.
Four-vector formulation
Relativistic four-momentum as proposed by Albert Einstein arises from the invariance of four-vectors under Lorentzian translation. The four-momentum P is defined as:The magnitude ||P|| of the momentum four-vector is equal to m0c, since
 and
and  , the respective final velocities
, the respective final velocities  and
and  may be found from the conservation of four-momentum which states that:
may be found from the conservation of four-momentum which states that:Generalization of momentum
Momentum is the Noether charge of translational invariance. As such, not just particles, but fields and other things can have momentum. However, where space–time is curved there is no Noether charge for translational invariance.Momentum in quantum mechanics
Further information: Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position and momentum are conjugate variables.For a single particle described in the position basis the momentum operator can be written as
Momentum in electromagnetism
Electric and magnetic fields possess momentum regardless of whether they are static or they change in time. The pressure, P, of an electrostatic (magnetostatic) field upon a metal sphere, cylindrical capacitor or ferromagnetic bar is: ,
,  ,
,  , are the electromagnetic energy density, electric field, and magnetic field respectively. The electromagnetic pressure
, are the electromagnetic energy density, electric field, and magnetic field respectively. The electromagnetic pressure  may be sufficiently high to explode the capacitor. Thus electric and magnetic fields do carry momentum.
may be sufficiently high to explode the capacitor. Thus electric and magnetic fields do carry momentum.Light (visible, UV, radio) is an electromagnetic wave and also has momentum. Even though photons (the particle aspect of light) have no mass, they still carry momentum. This leads to applications such as the solar sail. The calculation of the momentum of light within dielectric media is somewhat controversial (see Abraham–Minkowski controversy [2]).
Momentum is conserved in an electrodynamic system (it may change from momentum in the fields to mechanical momentum of moving parts). The treatment of the momentum of a field is usually accomplished by considering the so-called energy-momentum tensor and the change in time of the Poynting vector integrated over some volume. This is a tensor field which has components related to the energy density and the momentum density.
The definition canonical momentum corresponding to the momentum operator of quantum mechanics when it interacts with the electromagnetic field is, using the principle of least coupling:
 ,
,
 is the electromagnetic vector potential
is the electromagnetic vector potential the charged particle's invariant mass
the charged particle's invariant mass its velocity
its velocity its charge.
its charge.
Analogies between heat, mass, and momentum transfer
Main article: Transport phenomena
There are some notable similarities in equations for momentum, heat, and mass transfer.[16] The molecular transfer equations of Newton's law for fluid momentum, Fourier's law for heat, and Fick's law for mass are very similar. A great deal of effort has been devoted to developing analogies among these three transport processes so as to allow prediction of one from any of the others.



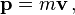












![\frac{d}{dt}\int \rho\,v_i\, dV =\int \left[ \left(\rho\frac{\partial v_i}{\partial t}+v_i\frac{\partial \rho}{\partial t}\right)+\partial_k (\rho v_i v_k)\right]\, dV\,.](http://upload.wikimedia.org/math/3/4/a/34a684a8c90a880f2676dd7d18dfdc22.png)
![\frac{d}{dt}\int \rho\,v_i\, dV=\int\rho\left[\frac{\partial}{\partial t}+v_k\partial_k\right]v_i\,dV +\int\left[\frac{\partial\rho}{\partial t}+\partial_k(\rho v_k)\right]v_i\,dV\,.](http://upload.wikimedia.org/math/c/e/e/ceea95058cccf42fc26379141158516a.png)

![\int_V \left[ \partial_j\sigma_{ij} + F_i - \rho \frac{D v_i}{Dt}\right]\, dV = 0\,.](http://upload.wikimedia.org/math/2/a/b/2ab5b365d6500b2bee0a8a390aa32a66.png)



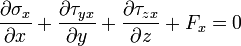

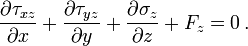











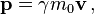



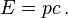







![P_{static} = {W}= \left[ {\epsilon_0 \epsilon}{\frac{{\mathbf E}^2 }{ {2}}} +{\frac{ 1 }{ {\mu_0 \mu} }} {\frac{{\mathbf B}^2}{{2}}} \right]\,,](http://upload.wikimedia.org/math/9/1/5/9154420d33b1874c32abf5a37f957802.png)

No comments:
Post a Comment