The Dulong–Petit law, a chemical law proposed in 1819 by French physical chemists Pierre Louis Dulong and Alexis Thérèse Petit, states the classical expression for the specific heat capacity of a crystal. Experimentally the two scientists had found that the heat capacity per weight (the mass-specific heat capacity) for a number of substances was close to a constant value, after it had been multiplied by the presumed weights of the atoms of the substance. These atomic weights had recently been suggested by Dalton.
The modern theory of the heat capacity of solids states that it is due to lattice vibrations in the solid, and was first derived in crude form from this assumption by Albert Einstein, in 1907. The Einstein solid model thus gave for the first time a reason why the Dulong-Petit law should be stated in terms of the classical heat capacities for gases.
Dulong and Petit did not state their law in terms of the gas constant R (which was not then known). Instead, they measured the values of heat capacities (per weight) of substances and found them smaller for substances of greater "atomic weight" as inferred by Dalton. Dulong and Petit then found that when multiplied by these atomic weights, the value for the heat capacity (which would now be the heat capacity PER MOLE in modern terms) was nearly constant, and equal to a value which was later recognized to be 3 R.
In other modern terminology, the dimensionless heat capacity is equal to 3.
Thus we have
The modern theory of the heat capacity of solids states that it is due to lattice vibrations in the solid, and was first derived in crude form from this assumption by Albert Einstein, in 1907. The Einstein solid model thus gave for the first time a reason why the Dulong-Petit law should be stated in terms of the classical heat capacities for gases.
Contents |
Equivalent forms of statement of the law
An equivalent statement of the Dulong-Petit law in modern terms is that, regardless of the nature of the substance or crystal, the specific heat capacity (measured in joule per kelvin per kilogram) is equal to 3R/M, where R is the gas constant (measured in joule per kelvin per mole) and M is the molar mass (measured in gram per mole).Dulong and Petit did not state their law in terms of the gas constant R (which was not then known). Instead, they measured the values of heat capacities (per weight) of substances and found them smaller for substances of greater "atomic weight" as inferred by Dalton. Dulong and Petit then found that when multiplied by these atomic weights, the value for the heat capacity (which would now be the heat capacity PER MOLE in modern terms) was nearly constant, and equal to a value which was later recognized to be 3 R.
In other modern terminology, the dimensionless heat capacity is equal to 3.
Application limits
Despite its simplicity, Dulong–Petit law offers fairly good prediction for the specific heat capacity of solids with relatively simple crystal structure at high temperatures. It fails, however, at room temperatures for light atoms bonded strongly to each other, such as in metallic beryllium, and in carbon as diamond. In the very low (cryogenic) temperature region, where the quantum mechanical nature of energy storage in all solids manifests itself with larger and larger effect, the law fails for all substances. For crystals under such conditions, the Debye model, an extension of the Einstein theory that accounts for statistical distributions in atomic vibration when there are lower amounts of energy to distribute, works well.Derivation
A system of vibrations in a crystalline solid lattice can be modelled by considering harmonic oscillator potentials along each degree of freedom. Then, the free energy of the system can be written as[1]Thus we have



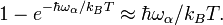



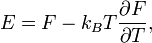


No comments:
Post a Comment