| Thermodynamics | ||||||||||

| ||||||||||
The law expresses that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed. It is usually formulated by stating that the change in the internal energy of a system is equal to the amount of heat supplied to the system, minus the amount of work performed by the system on its surroundings.
Contents |
Classical statement
The first explicit statement of the first law of thermodynamics was given by Rudolf Clausius in 1850:- "There is a state function E, called ‘energy’, whose differential equals the work exchanged with the surroundings during an adiabatic process."
Description
The first law of thermodynamics says that energy is conserved in any process involving a thermodynamic system and its surroundings. Frequently it is convenient to focus on changes in the assumed internal energy (U) and to regard them as due to a combination of heat (Q) added to the system and work done by the system (W). Taking dU as an infinitesimal (differential) change in internal energy, one writesWhen a system expands in a quasistatic process, the work done on the environment is the product of pressure (P) and volume (V) change, i.e. PdV, whereas the work done on the system is -PdV. The change in internal energy of the system is:
Informally, the law was first formulated by Germain Hess via Hess's Law, and later by Julius Robert von Mayer[1]
Adiabatic processes
The classical statement of the first law of thermodynamics is induced from empirical evidence. It can be observed that given a system in an initial state, if work is exerted on the system in an adiabatic (i.e. thermally insulated) way, the final state is the same for a given amount of work, irrespective of how this work is performed.For instance, in Joule's experiment, the initial system is a tank of water with a paddle wheel inside. If we isolate thermally the tank and move the paddle wheel with a pulley and a weight we can relate the increase in temperature with the height descended by the mass. Now the system is returned to its initial state, isolated again, and the same amount of work is done on the tank using different devices (an electric motor, a chemical battery, a spring,...). In every case, the amount of work can be measured independently. The evidence shows that the final state of the water (in particular, its temperature) is the same in every case. It's irrelevant if the work is electrical, mechanical, chemical,... or if done suddenly or slowly, as long as it is performed in an adiabatic way.
This evidence leads to the classical statement of the first law of thermodynamics
- For all adiabatic processes between two specified states of a closed system, the net work done is the same regardless of the nature of the closed system and the details of the process.
To go from a state A to a state B we can take a path that goes through the reference state, since the adiabatic work is independent of the path
- The internal energy of an isolated system remains constant.
Diabatic processes
See also: Thermodynamic processes
When the system does not evolve adiabatically, it is observed that the work exerted on the system does not coincide with the increase in its internal energy, which, being a state function, can be used for both adiabatic and non-adiabatic processes.State functional formulation
The infinitesimal heat and work in the equations above are denoted by δ, rather than exact differentials denoted by d, because they do not describe the state of any system. The integral of an inexact differential depends upon the particular path taken through the space of thermodynamic parameters while the integral of an exact differential depends only upon the initial and final states. If the initial and final states are the same, then the integral of an inexact differential may or may not be zero, but the integral of an exact differential will always be zero. The path taken by a thermodynamic system through a chemical or physical change is known as a thermodynamic process.An expression of the first law can be written in terms of exact differentials by realizing that the work that a system does is, in case of a reversible process, equal to its pressure times the infinitesimal change in its volume. In other words δw = PdV where P is pressure and V is volume. Also, for a reversible process, the total amount of heat added to a system can be expressed as δQ = TdS where T is temperature and S is entropy. Therefore, for a reversible process:
In the case where the number of particles in the system is not necessarily constant and may be of different types, the first law is written:
A useful idea from mechanics is that the energy gained by a particle is equal to the force applied to the particle multiplied by the displacement of the particle while that force is applied. Now consider the first law without the heating term: dU = − PdV. The pressure P can be viewed as a force (and in fact has units of force per unit area) while dV is the displacement (with units of distance times area). We may say, with respect to this work term, that a pressure difference forces a transfer of volume, and that the product of the two (work) is the amount of energy transferred as a result of the process.
It is useful to view the TdS term in the same light: With respect to this heat term, a temperature difference forces a transfer of entropy, and the product of the two (heat) is the amount of energy transferred as a result of the process. Here, the temperature is known as a "generalized" force (rather than an actual mechanical force) and the entropy is a generalized displacement.
Similarly, a difference in chemical potential between groups of particles in the system forces a transfer of particles, and the corresponding product is the amount of energy transferred as a result of the process. For example, consider a system consisting of two phases: liquid water and water vapor. There is a generalized "force" of evaporation which drives water molecules out of the liquid. There is a generalized "force" of condensation which drives vapor molecules out of the vapor. Only when these two "forces" (or chemical potentials) are equal will there be equilibrium, and the net transfer will be zero.
The two thermodynamic parameters which form a generalized force-displacement pair are termed "conjugate variables". The two most familiar pairs are, of course, pressure-volume, and temperature-entropy.




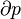
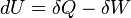




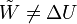
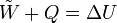




No comments:
Post a Comment