In chemistry, Henry's law is one of the gas laws, formulated by William Henry in 1803. It states that:
An everyday example of Henry's law is given by carbonated soft drinks. Before the bottle or can is opened, the gas above the drink is almost pure carbon dioxide at a pressure slightly higher than atmospheric pressure. The drink itself contains dissolved carbon dioxide. When the bottle or can is opened, some of this gas escapes, giving the characteristic hiss (or "pop" in the case of a champagne bottle). Because the pressure above the liquid is now lower, some of the dissolved carbon dioxide comes out of solution as bubbles. If a glass of the drink is left in the open, the concentration of carbon dioxide in solution will come into equilibrium with the carbon dioxide in the air, and the drink will go "flat".
Some values for kH for gases dissolved in water at 298 K include:
There are other forms of Henry's Law, each of which defines the constant kH differently and requires different dimensional units.[2] In particular, the "concentration" of the solute in solution may also be expressed as a mole fraction or as a molality.[1]
where:
It should also be noted the Henry's Law is a limiting law that only applies for sufficiently dilute solutions. The range of concentrations in which it applies becomes narrower the more the system diverges from ideal behavior. Roughly speaking, that is the more chemically different the solute is from the solvent.
It also only applies simply for solutions where the solvent does not react chemically with the gas being dissolved. A common example of a gas that does react with the solvent is carbon dioxide, which forms carbonic acid (H2CO3) to a certain degree with water.
The following table lists some values for constant C (in kelvins) in the equation above:
Because solubility of permanent gases usually decreases with increasing temperature at around the room temperature, the partial pressure a given gas concentration has in liquid must increase. While heating water (saturated with nitrogen) from 25 °C to 95 °C the solubility will decrease to about 43% of its initial value. This can be verified when heating water in a pot: small bubbles evolve and rise, long before the water reaches boiling temperature. Similarly, carbon dioxide from a carbonated drink escapes much faster when the drink is not cooled because of the increased partial pressure of CO2 in higher temperatures. Partial pressure of CO2 in the gas phase in equilibrium with seawater doubles with every 16 K increase in temperature.[5]
The constant C may be regarded as:
At first sight, Raoult's law appears to be a special case of Henry's law where kH = p*. This is true for pairs of closely related substances, such as benzene and toluene, which obey Raoult's law over the entire composition range: such mixtures are called "ideal mixtures".
The general case is that both laws are limit laws, and they apply at opposite ends of the composition range. The vapor pressure of the component in large excess, such as the solvent for a dilute solution, is proportional to its mole fraction, and the constant of proportionality is the vapor pressure of the pure substance (Raoult's law). The vapor pressure of the solute is also proportional to the solute's mole fraction, but the constant of proportionality is different and must be determined experimentally (Henry's law). In mathematical terms:
The standard state for a dilute solution is also defined in terms of infinite-dilution behavior. Although the standard concentration co is taken to be 1 mol/L by convention, the standard state is a hypothetical solution of 1 mol/L in which the solute has its limiting infinite-dilution properties. This has the effect that all non-ideal behavior is described by the activity coefficient: the activity coefficient at 1 mol/L is not necessarily unity (and is frequently quite different from unity).
All the relations above can also be expressed in terms of molalities rather than concentrations, e.g.:
o, the activity coefficient γm and the Henry's law constant kH,m all have different numerical values when molalities are used in place of concentrations.
- At a constant temperature, the amount of a given gas dissolved in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid.
An everyday example of Henry's law is given by carbonated soft drinks. Before the bottle or can is opened, the gas above the drink is almost pure carbon dioxide at a pressure slightly higher than atmospheric pressure. The drink itself contains dissolved carbon dioxide. When the bottle or can is opened, some of this gas escapes, giving the characteristic hiss (or "pop" in the case of a champagne bottle). Because the pressure above the liquid is now lower, some of the dissolved carbon dioxide comes out of solution as bubbles. If a glass of the drink is left in the open, the concentration of carbon dioxide in solution will come into equilibrium with the carbon dioxide in the air, and the drink will go "flat".
Contents |
Formula and the Henry's law constant
Henry's law can be put into mathematical terms (at constant temperature) asSome values for kH for gases dissolved in water at 298 K include:
There are other forms of Henry's Law, each of which defines the constant kH differently and requires different dimensional units.[2] In particular, the "concentration" of the solute in solution may also be expressed as a mole fraction or as a molality.[1]
Other forms of Henry's law
There are various other forms of Henry's Law which are discussed in the technical literature.[2][3][4]| equation: |  | 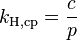 |  |  |
|---|---|---|---|---|
| units: |  |  | 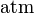 | dimensionless |
| O2 | 769.23 | 1.3×10−3 | 4.259×104 | 3.180×10−2 |
| H2 | 1282.05 | 7.8×10−4 | 7.099×104 | 1.907×10−2 |
| CO2 | 29.41 | 3.4×10−2 | 0.163×104 | 0.8317 |
| N2 | 1639.34 | 6.1×10−4 | 9.077×104 | 1.492×10−2 |
| He | 2702.7 | 3.7×10−4 | 14.97×104 | 9.051×10−3 |
| Ne | 2222.22 | 4.5×10−4 | 12.30×104 | 1.101×10−2 |
| Ar | 714.28 | 1.4×10−3 | 3.955×104 | 3.425×10−2 |
| CO | 1052.63 | 9.5×10−4 | 5.828×104 | 2.324×10−2 |
- c = amount concentration of gas in solution (in mol/L)
- p = partial pressure of gas above the solution (in atm)
- x = mole fraction of gas in solution (dimensionless)
It should also be noted the Henry's Law is a limiting law that only applies for sufficiently dilute solutions. The range of concentrations in which it applies becomes narrower the more the system diverges from ideal behavior. Roughly speaking, that is the more chemically different the solute is from the solvent.
It also only applies simply for solutions where the solvent does not react chemically with the gas being dissolved. A common example of a gas that does react with the solvent is carbon dioxide, which forms carbonic acid (H2CO3) to a certain degree with water.
Temperature dependence of the Henry constant
When the temperature of a system changes, the Henry constant will also change.[2] This is why some people prefer to name it Henry coefficient. There are multiple equations assessing the effect of temperature on the constant. These examples are derived by integrating the van 't Hoff equation:[4]- kH for a given temperature is the Henry's Law constant (as defined in the first section of this article). Notice that the correct sign of C depends on whether kH,pc or kH,cp is used.
- T is the thermodynamic temperature,
- T
orefers to the standard temperature (298 K).
The following table lists some values for constant C (in kelvins) in the equation above:
| Gas | O2 | H2 | CO2 | N2 | He | Ne | Ar | CO |
| C(K) | 1700 | 500 | 2400 | 1300 | 230 | 490 | 1300 | 1300 |
The constant C may be regarded as:
- ΔsolvH is the enthalpy of solution
- R is the gas constant.
In geophysics
In geophysics, a version of Henry's law applies to the solubility of a noble gas in contact with silicate melt. One equation used is- C = the number concentrations of the solute gas in the melt and gas phases
- β = 1/kBT, an inverse temperature scale: kB = the Boltzmann constant
- µE = the excess chemical potentials of the solute gas in the two phases.
Comparison to Raoult's law
For a dilute solution, the concentration of the solute is approximately proportional to its mole fraction x, and Henry's law can be written as:At first sight, Raoult's law appears to be a special case of Henry's law where kH = p*. This is true for pairs of closely related substances, such as benzene and toluene, which obey Raoult's law over the entire composition range: such mixtures are called "ideal mixtures".
The general case is that both laws are limit laws, and they apply at opposite ends of the composition range. The vapor pressure of the component in large excess, such as the solvent for a dilute solution, is proportional to its mole fraction, and the constant of proportionality is the vapor pressure of the pure substance (Raoult's law). The vapor pressure of the solute is also proportional to the solute's mole fraction, but the constant of proportionality is different and must be determined experimentally (Henry's law). In mathematical terms:
- Raoult's law:
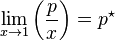
- Henry's law:
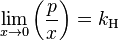
Standard chemical potential
Henry's law has been shown to apply to a wide range of solutes in the limit of "infinite dilution" (x→0), including non-volatile substances such as sucrose or even sodium chloride. In these cases, it is necessary to state the law in terms of chemical potentials. For a solute in an ideal dilute solution, the chemical potential depends on the concentration: , where
, where  for a volatile solute; c
for a volatile solute; co= 1 mol/L.
The standard state for a dilute solution is also defined in terms of infinite-dilution behavior. Although the standard concentration c
All the relations above can also be expressed in terms of molalities rather than concentrations, e.g.:
 , where
, where 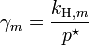 for a volatile solutes; m
for a volatile solutes; mo= 1 mol/kg.

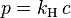
![k_{\rm H,pc}(T) = k_{\rm H,pc}(T^\ominus)\, \exp{ \left[ -C \, \left( \frac{1}{T}-\frac{1}{T^\ominus}\right)\right]}\,](http://upload.wikimedia.org/math/c/7/a/c7ab0d7f911ef2bd54a39a627b1c893d.png)
![k_{\rm H,cp}(T) = k_{\rm H,cp}(T^\ominus)\, \exp{ \left[ C \, \left( \frac{1}{T}-\frac{1}{T^\ominus}\right)\right]}\,](http://upload.wikimedia.org/math/5/3/c/53cb9ed152540ea821076c3d3f74f4ef.png)
![C = -\frac{\Delta_{\rm solv}H}{R} = -\frac{{\rm d}\left[ \ln k_{\rm H}(T)\right]}{{\rm d}(1/T)}](http://upload.wikimedia.org/math/b/4/5/b4568ac0d11bdf93d039d0def7bab37c.png)
![C_{\rm melt}/C_{\rm gas} = \exp\left[-\beta(\mu^{\rm E}_{\rm melt} - \mu^{\rm E}_{\rm gas})\right]\,](http://upload.wikimedia.org/math/8/0/e/80e500841fc90e87edd676bf0bac14d4.png)


No comments:
Post a Comment