| Thermodynamics | ||||||||||

| ||||||||||

Isotherms of an ideal gas. The curved lines represent the relationship between pressure (on the vertical, y-axis) and volume (on the horizontal, x-axis) for an ideal gas at different temperatures: lines which are further away from the origin (that is, lines that are nearer to the top right-hand corner of the diagram) represent higher temperatures.
The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation is:
In SI units, p is measured in pascals; V in cubic metres; n in moles; and T in kelvin. R has the value 8.314472 J·K−1·mol−1 in SI units[4]).
The temperature given in the equation of state must be an absolute temperature that begins at absolute zero. In the metric system of units, we must specify the temperature in Kelvin (degree increments as in Celsius). In the Imperial system, absolute temperature is in Rankine (degree increments as in Fahrenheit). [5]
Contents |
Deviations from real gases
The equation of state given here applies only to an ideal gas, or a real gas that behaves like an ideal gas. There are in fact many different forms for the equation of state for different gases. Since it neglects both molecular size and intermolecular attractions, the ideal gas law is most accurate for monatomic gases at high temperatures and low pressures. The neglect of molecular size becomes less important for lower densities, i.e. for larger volumes at lower pressures, because the average distance between adjacent molecules becomes much larger than the molecular size. The relative importance of intermolecular attractions diminishes with increasing thermal kinetic energy i.e., with increasing temperatures. More detailed equations of state, such as the van der Waals equation, allow deviations from ideality caused by molecular size and intermolecular forces to be taken into account.A residual property is defined as the difference between a real gas property and an ideal gas property, both considered at the same pressure, temperature, and composition.
Alternative forms
Molar form
As the amount of substance could be given in mass instead of moles, sometimes an alternative form of the ideal gas law is useful. The number of moles (n) is equal to the mass (m) divided by the molar mass (M): , we get:
, we get: .
.
Engineering
Some engineers use a slightly different form of the equation of state that is specialized for a particular gas and written in terms of specific volume[citation needed].A variation of the gas constant R is used, which is equal to the universal gas constant divided by the mass per mole of the gas. The value of the new constant depends on the type of gas, as opposed to the universal gas constant which is the same for all gases. In most engineering fields, R is written with a bar, as
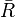 , so that a new symbol R is defined by
, so that a new symbol R is defined by  , where MW is the molecular weight.
, where MW is the molecular weight.If we divide both sides of the general ideal gas equation by the mass of the gas, the volume becomes the specific volume, which is the reciprocal of the gas density. The equation of state can be written in terms of the specific volume or in terms of the air density as
- pv = RT, or
- p = ρRT,
- ρ is the density [kg/m3] and v is the specific volume [m3/kg].
Statistical mechanics
In statistical mechanics the following molecular equation is derived from first principles:From here we can notice that for an average particle mass of μ times the atomic mass constant mu (i.e., the mass is μ u)
Applications to thermodynamics processes
The table below essentially simplifies the ideal gas equation for a particular processes, thus making this equation easier to solve using numerical methods.A thermodynamic process is defined as a system that moves from state 1 to state 2, where the state number is denoted by subscript. As shown in the first column of the table, basic thermodynamic processes are defined such that one of the gas properties (p, V, T, or S) is constant throughout the process.
For a given thermodynamics process, in order to specify the extent of a particular process, one of the properties ratios (listed under the column labeled "known ratio") must be specified (either directly or indirectly). Also, the property for which the ratio is known must be distinct from the property held constant in the previous column (otherwise the ratio would be unity, and not enough information would be available to simplify the gas law equation).
In the final three columns, the properties (p, V, or T) at state 2 can be calculated from the properties at state 1 using the equations listed.
| process | Constant | Known ratio | p2 | V2 | T2 |
|---|---|---|---|---|---|
| Isobaric process | | | p2 = p1 | V2 = V1(V2/V1) | T2 = T1(V2/V1) |
| | p2 = p1 | V2 = V1(T2/T1) | T2 = T1(T2/T1) | ||
| Isochoric process | | | p2 = p1(p2/p1) | V2 = V1 | T2 = T1(p2/p1) |
| | p2 = p1(T2/T1) | V2 = V1 | T2 = T1(T2/T1) | ||
| Isothermal process | | | p2 = p1(p2/p1) | V2 = V1/(p2/p1) | T2 = T1 |
| | p2 = p1/(V2/V1) | V2 = V1(V2/V1) | T2 = T1 | ||
| Isentropic process (Reversible adiabatic process) | | | p2 = p1(p2/p1) | V2 = V1(p2/p1)−1/γ | T2 = T1(p2/p1)(γ − 1)/γ |
| | p2 = p1(V2/V1)−γ | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − γ) | ||
| | p2 = p1(T2/T1)γ/(γ − 1) | V2 = V1(T2/T1)1/(1 − γ) | T2 = T1(T2/T1) |
Derivations
Empirical
The ideal gas law can be derived from combining two empirical gas laws: the combined gas law and Avogadro's law. The combined gas law states thatHence the ideal gas law
Theoretical
The ideal gas law can also be derived from first principles using the kinetic theory of gases, in which several simplifying assumptions are made, chief among which are that the molecules, or atoms, of the gas are point masses, possessing mass but no significant volume, and undergo only elastic collisions with each other and the sides of the container in which both linear momentum and kinetic energy are conserved.From statistical mechanics
Let q = (qx, qy, qz) and p = (px, py, pz) denote the position vector and momentum vector of a particle of an ideal gas, respectively. Let F denote the net force on that particle. Then the time average momentum of the particle is:
where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of N particles yields
Putting these equalities together yields
The readers are referred to the comprehensive article Configuration integral (statistical mechanics) where an alternative statistical mechanics derivation of the ideal-gas law, using the relationship between the Helmholtz free energy and the partition function, but without using the equipartition theorem, is provided.




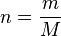


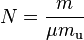
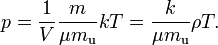







No comments:
Post a Comment